Quantum Monte Carlo
Table of Contents
- 1. Introduction
- 2. Numerical evaluation of the energy
- 3. Variational Monte Carlo
- 4. Diffusion Monte Carlo
- 5. TODO
[0/1]Last things to do
1 Introduction
This web site is the QMC tutorial of the LTTC winter school Tutorials in Theoretical Chemistry.
We propose different exercises to understand quantum Monte Carlo (QMC) methods. In the first section, we propose to compute the energy of a hydrogen atom using numerical integration. The goal of this section is to introduce the local energy. Then we introduce the variational Monte Carlo (VMC) method which computes a statistical estimate of the expectation value of the energy associated with a given wave function. Finally, we introduce the diffusion Monte Carlo (DMC) method which gives the exact energy of the hydrogen atom and of the \(H_2\) molecule.
Code examples will be given in Python and Fortran. You can use whatever language you prefer to write the program.
We consider the stationary solution of the Schrödinger equation, so the wave functions considered here are real: for an \(N\) electron system where the electrons move in the 3-dimensional space, \(\Psi : \mathbb{R}^{3N} \rightarrow \mathbb{R}\). In addition, \(\Psi\) is defined everywhere, continuous and infinitely differentiable.
All the quantities are expressed in atomic units (energies, coordinates, etc).
2 Numerical evaluation of the energy
In this section we consider the Hydrogen atom with the following wave function:
\[ \Psi(\mathbf{r}) = \exp(-a |\mathbf{r}|) \]
We will first verify that, for a given value of \(a\), \(\Psi\) is an eigenfunction of the Hamiltonian
\[ \hat{H} = \hat{T} + \hat{V} = - \frac{1}{2} \Delta - \frac{1}{|\mathbf{r}|} \]
To do that, we will check if the local energy, defined as
\[ E_L(\mathbf{r}) = \frac{\hat{H} \Psi(\mathbf{r})}{\Psi(\mathbf{r})}, \]
is constant.
The probabilistic expected value of an arbitrary function \(f(x)\) with respect to a probability density function \(p(x)\) is given by
\[ \langle f \rangle_p = \int_{-\infty}^\infty p(x)\, f(x)\,dx. \]
Recall that a probability density function \(p(x)\) is non-negative and integrates to one:
\[ \int_{-\infty}^\infty p(x)\,dx = 1. \]
The electronic energy of a system is the expectation value of the local energy \(E(\mathbf{r})\) with respect to the 3N-dimensional electron density given by the square of the wave function:
\begin{eqnarray*} E & = & \frac{\langle \Psi| \hat{H} | \Psi\rangle}{\langle \Psi |\Psi \rangle} = \frac{\int \Psi(\mathbf{r})\, \hat{H} \Psi(\mathbf{r})\, d\mathbf{r}}{\int \left[\Psi(\mathbf{r}) \right]^2 d\mathbf{r}} \\ & = & \frac{\int \left[\Psi(\mathbf{r})\right]^2\, \frac{\hat{H} \Psi(\mathbf{r})}{\Psi(\mathbf{r})}\,d\mathbf{r}}{\int \left[\Psi(\mathbf{r}) \right]^2 d\mathbf{r}} = \frac{\int \left[\Psi(\mathbf{r})\right]^2\, E_L(\mathbf{r})\,d\mathbf{r}}{\int \left[\Psi(\mathbf{r}) \right]^2 d\mathbf{r}} = \langle E_L \rangle_{\Psi^2} \end{eqnarray*}2.1 Local energy
Write all the functions of this section in a single file :
hydrogen.py if you use Python, or hydrogen.f90 is you use
Fortran.
- When computing a square root in \(\mathbb{R}\), always make sure that the argument of the square root is non-negative.
- When you divide, always make sure that you will not divide by zero
If a floating-point exception can occur, you should make a test to catch the error.
2.1.1 Exercise 1
Write a function which computes the potential at \(\mathbf{r}\).
The function accepts a 3-dimensional vector r as input arguments
and returns the potential.
\(\mathbf{r}=\left( \begin{array}{c} x \\ y\\ z\end{array} \right)\), so \[ V(\mathbf{r}) = -\frac{1}{\sqrt{x^2 + y^2 + z^2}} \]
Python
import numpy as np def potential(r): # TODO
Fortran
double precision function potential(r) implicit none double precision, intent(in) :: r(3) ! TODO end function potential
2.1.1.1 Solution solution
Python
import numpy as np def potential(r): distance = np.sqrt(np.dot(r,r)) assert (distance > 0) return -1. / distance
Fortran
double precision function potential(r) implicit none double precision, intent(in) :: r(3) double precision :: distance distance = dsqrt( r(1)*r(1) + r(2)*r(2) + r(3)*r(3) ) if (distance > 0.d0) then potential = -1.d0 / dsqrt( r(1)*r(1) + r(2)*r(2) + r(3)*r(3) ) else stop 'potential at r=0.d0 diverges' end if end function potential
2.1.2 Exercise 2
Write a function which computes the wave function at \(\mathbf{r}\).
The function accepts a scalar a and a 3-dimensional vector r as
input arguments, and returns a scalar.
Python
def psi(a, r): # TODO
Fortran
double precision function psi(a, r) implicit none double precision, intent(in) :: a, r(3) ! TODO end function psi
2.1.2.1 Solution solution
Python
def psi(a, r): return np.exp(-a*np.sqrt(np.dot(r,r)))
Fortran
double precision function psi(a, r) implicit none double precision, intent(in) :: a, r(3) psi = dexp(-a * dsqrt( r(1)*r(1) + r(2)*r(2) + r(3)*r(3) )) end function psi
2.1.3 Exercise 3
Write a function which computes the local kinetic energy at \(\mathbf{r}\).
The function accepts a and r as input arguments and returns the
local kinetic energy.
The local kinetic energy is defined as \[-\frac{1}{2}\frac{\Delta \Psi}{\Psi}.\]
We differentiate \(\Psi\) with respect to \(x\):
\[\Psi(\mathbf{r}) = \exp(-a\,|\mathbf{r}|) \] \[\frac{\partial \Psi}{\partial x} = \frac{\partial \Psi}{\partial |\mathbf{r}|} \frac{\partial |\mathbf{r}|}{\partial x} = - \frac{a\,x}{|\mathbf{r}|} \Psi(\mathbf{r}) \]
and we differentiate a second time:
\[ \frac{\partial^2 \Psi}{\partial x^2} = \left( \frac{a^2\,x^2}{|\mathbf{r}|^2} - \frac{a(y^2+z^2)}{|\mathbf{r}|^{3}} \right) \Psi(\mathbf{r}). \]
The Laplacian operator \(\Delta = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\) applied to the wave function gives:
\[ \Delta \Psi (\mathbf{r}) = \left(a^2 - \frac{2a}{\mathbf{|r|}} \right) \Psi(\mathbf{r}) \]
So the local kinetic energy is \[ -\frac{1}{2} \frac{\Delta \Psi}{\Psi} (\mathbf{r}) = -\frac{1}{2}\left(a^2 - \frac{2a}{\mathbf{|r|}} \right) \]
Python
def kinetic(a,r): # TODO
Fortran
double precision function kinetic(a,r) implicit none double precision, intent(in) :: a, r(3) ! TODO end function kinetic
2.1.3.1 Solution solution
Python
def kinetic(a,r): distance = np.sqrt(np.dot(r,r)) assert (distance > 0.) return -0.5 * (a**2 - (2.*a)/distance)
Fortran
double precision function kinetic(a,r) implicit none double precision, intent(in) :: a, r(3) double precision :: distance distance = dsqrt( r(1)*r(1) + r(2)*r(2) + r(3)*r(3) ) if (distance > 0.d0) then kinetic = -0.5d0 * (a*a - (2.d0*a) / distance) else stop 'kinetic energy diverges at r=0' end if end function kinetic
2.1.4 Exercise 4
Write a function which computes the local energy at \(\mathbf{r}\),
using the previously defined functions.
The function accepts a and r as input arguments and returns the
local kinetic energy.
\[ E_L(\mathbf{r}) = -\frac{1}{2} \frac{\Delta \Psi}{\Psi} (\mathbf{r}) + V(\mathbf{r}) \]
Python
def e_loc(a,r): #TODO
Fortran
double precision function e_loc(a,r) implicit none double precision, intent(in) :: a, r(3) ! TODO end function e_loc
2.1.4.1 Solution solution
Python
def e_loc(a,r): return kinetic(a,r) + potential(r)
Fortran
double precision function e_loc(a,r) implicit none double precision, intent(in) :: a, r(3) double precision, external :: kinetic, potential e_loc = kinetic(a,r) + potential(r) end function e_loc
2.1.5 Exercise 5
Find the theoretical value of \(a\) for which \(\Psi\) is an eigenfunction of \(\hat{H}\).
2.1.5.1 Solution solution
\(a=1\) cancels the \(1/|r|\) term, and makes the energy constant, equal to -0.5 atomic units.
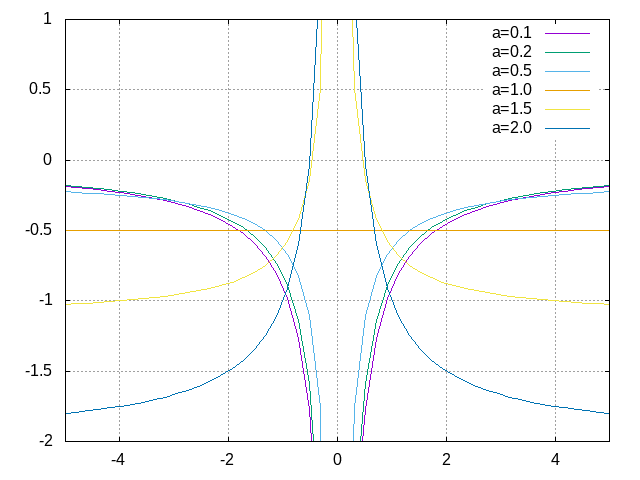
2.2 Plot of the local energy along the \(x\) axis
The potential and the kinetic energy both diverge at \(r=0\), so we choose a grid which does not contain the origin.
2.2.1 Exercise
For multiple values of \(a\) (0.1, 0.2, 0.5, 1., 1.5, 2.), plot the local energy along the \(x\) axis. In Python, you can use matplotlib for example. In Fortran, it is convenient to write in a text file the values of \(x\) and \(E_L(\mathbf{r})\) for each point, and use Gnuplot to plot the files.
Python
import numpy as np import matplotlib.pyplot as plt from hydrogen import e_loc x=np.linspace(-5,5) plt.figure(figsize=(10,5)) # TODO plt.tight_layout() plt.legend() plt.savefig("plot_py.png")
Fortran
program plot implicit none double precision, external :: e_loc double precision :: x(50), dx integer :: i, j dx = 10.d0/(size(x)-1) do i=1,size(x) x(i) = -5.d0 + (i-1)*dx end do ! TODO end program plot
To compile and run:
gfortran hydrogen.f90 plot_hydrogen.f90 -o plot_hydrogen ./plot_hydrogen > data
To plot the data using Gnuplot:
set grid
set xrange [-5:5]
set yrange [-2:1]
plot './data' index 0 using 1:2 with lines title 'a=0.1', \
'./data' index 1 using 1:2 with lines title 'a=0.2', \
'./data' index 2 using 1:2 with lines title 'a=0.5', \
'./data' index 3 using 1:2 with lines title 'a=1.0', \
'./data' index 4 using 1:2 with lines title 'a=1.5', \
'./data' index 5 using 1:2 with lines title 'a=2.0'
2.2.1.1 Solution solution
Python
import numpy as np import matplotlib.pyplot as plt from hydrogen import e_loc x=np.linspace(-5,5) plt.figure(figsize=(10,5)) for a in [0.1, 0.2, 0.5, 1., 1.5, 2.]: y=np.array([ e_loc(a, np.array([t,0.,0.]) ) for t in x]) plt.plot(x,y,label=f"a={a}") plt.tight_layout() plt.legend() plt.savefig("plot_py.png")
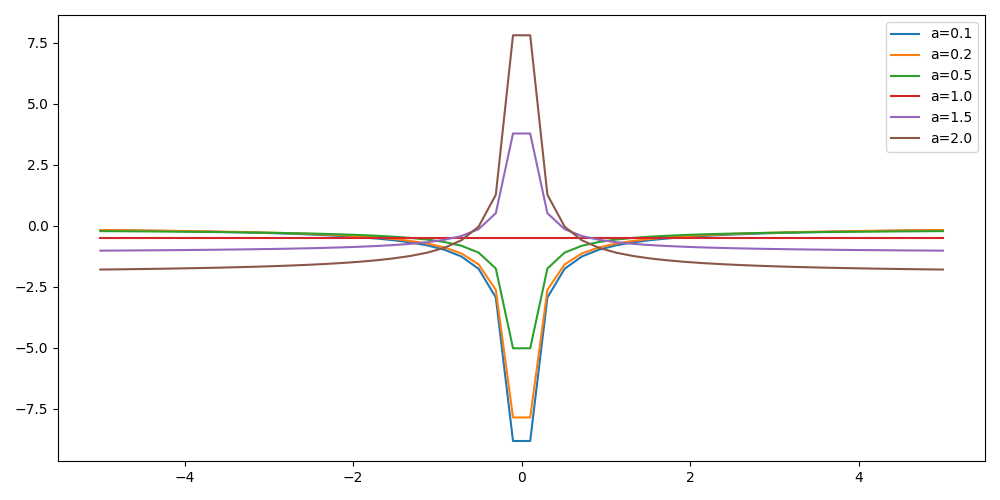
Fortran
program plot implicit none double precision, external :: e_loc double precision :: x(50), energy, dx, r(3), a(6) integer :: i, j a = (/ 0.1d0, 0.2d0, 0.5d0, 1.d0, 1.5d0, 2.d0 /) dx = 10.d0/(size(x)-1) do i=1,size(x) x(i) = -5.d0 + (i-1)*dx end do r(:) = 0.d0 do j=1,size(a) print *, '# a=', a(j) do i=1,size(x) r(1) = x(i) energy = e_loc( a(j), r ) print *, x(i), energy end do print *, '' print *, '' end do end program plot
2.3 Numerical estimation of the energy
If the space is discretized in small volume elements \(\mathbf{r}_i\) of size \(\delta \mathbf{r}\), the expression of \(\langle E_L \rangle_{\Psi^2}\) becomes a weighted average of the local energy, where the weights are the values of the probability density at \(\mathbf{r}_i\) multiplied by the volume element:
\[ \langle E \rangle_{\Psi^2} \approx \frac{\sum_i w_i E_L(\mathbf{r}_i)}{\sum_i w_i}, \;\; w_i = \left[\Psi(\mathbf{r}_i)\right]^2 \delta \mathbf{r} \]
The energy is biased because:
- The volume elements are not infinitely small (discretization error)
- The energy is evaluated only inside the box (incompleteness of the space)
2.3.1 Exercise
Compute a numerical estimate of the energy in a grid of \(50\times50\times50\) points in the range \((-5,-5,-5) \le \mathbf{r} \le (5,5,5)\).
Python
import numpy as np from hydrogen import e_loc, psi interval = np.linspace(-5,5,num=50) delta = (interval[1]-interval[0])**3 r = np.array([0.,0.,0.]) for a in [0.1, 0.2, 0.5, 0.9, 1., 1.5, 2.]: # TODO print(f"a = {a} \t E = {E}")
Fortran
program energy_hydrogen implicit none double precision, external :: e_loc, psi double precision :: x(50), w, delta, energy, dx, r(3), a(6), norm integer :: i, k, l, j a = (/ 0.1d0, 0.2d0, 0.5d0, 1.d0, 1.5d0, 2.d0 /) dx = 10.d0/(size(x)-1) do i=1,size(x) x(i) = -5.d0 + (i-1)*dx end do do j=1,size(a) ! TODO print *, 'a = ', a(j), ' E = ', energy end do end program energy_hydrogen
To compile the Fortran and run it:
gfortran hydrogen.f90 energy_hydrogen.f90 -o energy_hydrogen ./energy_hydrogen
2.3.1.1 Solution solution
Python
import numpy as np from hydrogen import e_loc, psi interval = np.linspace(-5,5,num=50) delta = (interval[1]-interval[0])**3 r = np.array([0.,0.,0.]) for a in [0.1, 0.2, 0.5, 0.9, 1., 1.5, 2.]: E = 0. norm = 0. for x in interval: r[0] = x for y in interval: r[1] = y for z in interval: r[2] = z w = psi(a,r) w = w * w * delta E += w * e_loc(a,r) norm += w E = E / norm print(f"a = {a} \t E = {E}")
a = 0.1 E = -0.24518438948809218 a = 0.2 E = -0.26966057967803525 a = 0.5 E = -0.3856357612517407 a = 0.9 E = -0.49435709786716214 a = 1.0 E = -0.5 a = 1.5 E = -0.39242967082602226 a = 2.0 E = -0.08086980667844901
Fortran
program energy_hydrogen implicit none double precision, external :: e_loc, psi double precision :: x(50), w, delta, energy, dx, r(3), a(6), norm integer :: i, k, l, j a = (/ 0.1d0, 0.2d0, 0.5d0, 1.d0, 1.5d0, 2.d0 /) dx = 10.d0/(size(x)-1) do i=1,size(x) x(i) = -5.d0 + (i-1)*dx end do delta = dx**3 r(:) = 0.d0 do j=1,size(a) energy = 0.d0 norm = 0.d0 do i=1,size(x) r(1) = x(i) do k=1,size(x) r(2) = x(k) do l=1,size(x) r(3) = x(l) w = psi(a(j),r) w = w * w * delta energy = energy + w * e_loc(a(j), r) norm = norm + w end do end do end do energy = energy / norm print *, 'a = ', a(j), ' E = ', energy end do end program energy_hydrogen
a = 0.10000000000000001 E = -0.24518438948809140 a = 0.20000000000000001 E = -0.26966057967803236 a = 0.50000000000000000 E = -0.38563576125173815 a = 1.0000000000000000 E = -0.50000000000000000 a = 1.5000000000000000 E = -0.39242967082602065 a = 2.0000000000000000 E = -8.0869806678448772E-002
2.4 Variance of the local energy
The variance of the local energy is a functional of \(\Psi\) which measures the magnitude of the fluctuations of the local energy associated with \(\Psi\) around its average:
\[ \sigma^2(E_L) = \frac{\int \left[\Psi(\mathbf{r})\right]^2\, \left[ E_L(\mathbf{r}) - E \right]^2 \, d\mathbf{r}}{\int \left[\Psi(\mathbf{r}) \right]^2 d\mathbf{r}} \] which can be simplified as
\[ \sigma^2(E_L) = \langle E_L^2 \rangle_{\Psi^2} - \langle E_L \rangle_{\Psi^2}^2.\]
If the local energy is constant (i.e. \(\Psi\) is an eigenfunction of \(\hat{H}\)) the variance is zero, so the variance of the local energy can be used as a measure of the quality of a wave function.
2.4.1 Exercise (optional)
Prove that : \[\left( \langle E - \langle E \rangle_{\Psi^2} \rangle_{\Psi^2} \right)^2 = \langle E^2 \rangle_{\Psi^2} - \langle E \rangle_{\Psi^2}^2 \]
2.4.1.1 TODO Solution solution
2.4.2 Exercise
Add the calculation of the variance to the previous code, and compute a numerical estimate of the variance of the local energy in a grid of \(50\times50\times50\) points in the range \((-5,-5,-5) \le \mathbf{r} \le (5,5,5)\) for different values of \(a\).
Python
import numpy as np from hydrogen import e_loc, psi interval = np.linspace(-5,5,num=50) delta = (interval[1]-interval[0])**3 r = np.array([0.,0.,0.]) for a in [0.1, 0.2, 0.5, 0.9, 1., 1.5, 2.]: # TODO print(f"a = {a} \t E = {E:10.8f} \t \sigma^2 = {s2:10.8f}")
Fortran
program variance_hydrogen implicit none double precision, external :: e_loc, psi double precision :: x(50), w, delta, energy, dx, r(3), a(6), norm, s2 double precision :: e, energy2 integer :: i, k, l, j a = (/ 0.1d0, 0.2d0, 0.5d0, 1.d0, 1.5d0, 2.d0 /) dx = 10.d0/(size(x)-1) do i=1,size(x) x(i) = -5.d0 + (i-1)*dx end do delta = dx**3 r(:) = 0.d0 do j=1,size(a) ! TODO print *, 'a = ', a(j), ' E = ', energy, ' s2 = ', s2 end do end program variance_hydrogen
To compile and run:
gfortran hydrogen.f90 variance_hydrogen.f90 -o variance_hydrogen ./variance_hydrogen
2.4.2.1 Solution solution
Python
import numpy as np from hydrogen import e_loc, psi interval = np.linspace(-5,5,num=50) delta = (interval[1]-interval[0])**3 r = np.array([0.,0.,0.]) for a in [0.1, 0.2, 0.5, 0.9, 1., 1.5, 2.]: E = 0. E2 = 0. norm = 0. for x in interval: r[0] = x for y in interval: r[1] = y for z in interval: r[2] = z w = psi(a, r) w = w * w * delta El = e_loc(a, r) E += w * El E2 += w * El*El norm += w E = E / norm E2 = E2 / norm s2 = E2 - E*E print(f"a = {a} \t E = {E:10.8f} \t \sigma^2 = {s2:10.8f}")
a = 0.1 E = -0.24518439 \sigma^2 = 0.02696522 a = 0.2 E = -0.26966058 \sigma^2 = 0.03719707 a = 0.5 E = -0.38563576 \sigma^2 = 0.05318597 a = 0.9 E = -0.49435710 \sigma^2 = 0.00577812 a = 1.0 E = -0.50000000 \sigma^2 = 0.00000000 a = 1.5 E = -0.39242967 \sigma^2 = 0.31449671 a = 2.0 E = -0.08086981 \sigma^2 = 1.80688143
Fortran
program variance_hydrogen implicit none double precision, external :: e_loc, psi double precision :: x(50), w, delta, energy, dx, r(3), a(6), norm, s2 double precision :: e, energy2 integer :: i, k, l, j a = (/ 0.1d0, 0.2d0, 0.5d0, 1.d0, 1.5d0, 2.d0 /) dx = 10.d0/(size(x)-1) do i=1,size(x) x(i) = -5.d0 + (i-1)*dx end do delta = dx**3 r(:) = 0.d0 do j=1,size(a) energy = 0.d0 energy2 = 0.d0 norm = 0.d0 do i=1,size(x) r(1) = x(i) do k=1,size(x) r(2) = x(k) do l=1,size(x) r(3) = x(l) w = psi(a(j),r) w = w * w * delta e = e_loc(a(j), r) energy = energy + w * e energy2 = energy2 + w * e * e norm = norm + w end do end do end do energy = energy / norm energy2 = energy2 / norm s2 = energy2 - energy*energy print *, 'a = ', a(j), ' E = ', energy, ' s2 = ', s2 end do end program variance_hydrogen
a = 0.10000000000000001 E = -0.24518438948809140 s2 = 2.6965218719722767E-002 a = 0.20000000000000001 E = -0.26966057967803236 s2 = 3.7197072370201284E-002 a = 0.50000000000000000 E = -0.38563576125173815 s2 = 5.3185967578480653E-002 a = 1.0000000000000000 E = -0.50000000000000000 s2 = 0.0000000000000000 a = 1.5000000000000000 E = -0.39242967082602065 s2 = 0.31449670909172917 a = 2.0000000000000000 E = -8.0869806678448772E-002 s2 = 1.8068814270846534
3 Variational Monte Carlo
Numerical integration with deterministic methods is very efficient in low dimensions. When the number of dimensions becomes large, instead of computing the average energy as a numerical integration on a grid, it is usually more efficient to do a Monte Carlo sampling.
Moreover, a Monte Carlo sampling will alow us to remove the bias due to the discretization of space, and compute a statistical confidence interval.
3.1 Computation of the statistical error
To compute the statistical error, you need to perform \(M\) independent Monte Carlo calculations. You will obtain \(M\) different estimates of the energy, which are expected to have a Gaussian distribution according to the Central Limit Theorem.
The estimate of the energy is
\[ E = \frac{1}{M} \sum_{i=1}^M E_M \]
The variance of the average energies can be computed as
\[ \sigma^2 = \frac{1}{M-1} \sum_{i=1}^{M} (E_M - E)^2 \]
And the confidence interval is given by
\[ E \pm \delta E, \text{ where } \delta E = \frac{\sigma}{\sqrt{M}} \]
3.1.1 Exercise
Write a function returning the average and statistical error of an input array.
Python
from math import sqrt def ave_error(arr): #TODO return (average, error)
Fortran
subroutine ave_error(x,n,ave,err) implicit none integer, intent(in) :: n double precision, intent(in) :: x(n) double precision, intent(out) :: ave, err ! TODO end subroutine ave_error
3.1.1.1 Solution solution
Python
from math import sqrt def ave_error(arr): M = len(arr) assert(M>0) if M == 1: return (arr[0], 0.) else: average = sum(arr)/M variance = 1./(M-1) * sum( [ (x - average)**2 for x in arr ] ) error = sqrt(variance/M) return (average, error)
Fortran
subroutine ave_error(x,n,ave,err) implicit none integer, intent(in) :: n double precision, intent(in) :: x(n) double precision, intent(out) :: ave, err double precision :: variance if (n < 1) then stop 'n<1 in ave_error' else if (n == 1) then ave = x(1) err = 0.d0 else ave = sum(x(:)) / dble(n) variance = sum( (x(:) - ave)**2 ) / dble(n-1) err = dsqrt(variance/dble(n)) endif end subroutine ave_error
3.2 Uniform sampling in the box
We will now do our first Monte Carlo calculation to compute the energy of the hydrogen atom.
At every Monte Carlo iteration:
- Draw a random point \(\mathbf{r}_i\) in the box \((-5,-5,-5) \le (x,y,z) \le (5,5,5)\)
- Compute \([\Psi(\mathbf{r}_i)]^2\) and accumulate the result in a
variable
normalization - Compute \([\Psi(\mathbf{r}_i)]^2 \times E_L(\mathbf{r}_i)\), and accumulate the
result in a variable
energy
One Monte Carlo run will consist of \(N\) Monte Carlo iterations. Once all the iterations have been computed, the run returns the average energy \(\bar{E}_k\) over the \(N\) iterations of the run.
To compute the statistical error, perform \(M\) independent runs. The final estimate of the energy will be the average over the \(\bar{E}_k\), and the variance of the \(\bar{E}_k\) will be used to compute the statistical error.
3.2.1 Exercise
Parameterize the wave function with \(a=0.9\). Perform 30 independent Monte Carlo runs, each with 100 000 Monte Carlo steps. Store the final energies of each run and use this array to compute the average energy and the associated error bar.
Python
To draw a uniform random number in Python, you can use
the random.uniform function of Numpy.
from hydrogen import * from qmc_stats import * def MonteCarlo(a, nmax): # TODO a = 0.9 nmax = 100000 #TODO print(f"E = {E} +/- {deltaE}")
Fortran
To draw a uniform random number in Fortran, you can use
the RANDOM_NUMBER subroutine.
When running Monte Carlo calculations, the number of steps is
usually very large. We expect nmax to be possibly larger than 2
billion, so we use 8-byte integers (integer*8) to represent it, as
well as the index of the current step.
subroutine uniform_montecarlo(a,nmax,energy) implicit none double precision, intent(in) :: a integer*8 , intent(in) :: nmax double precision, intent(out) :: energy integer*8 :: istep double precision :: norm, r(3), w double precision, external :: e_loc, psi ! TODO end subroutine uniform_montecarlo program qmc implicit none double precision, parameter :: a = 0.9 integer*8 , parameter :: nmax = 100000 integer , parameter :: nruns = 30 integer :: irun double precision :: X(nruns) double precision :: ave, err !TODO print *, 'E = ', ave, '+/-', err end program qmc
gfortran hydrogen.f90 qmc_stats.f90 qmc_uniform.f90 -o qmc_uniform ./qmc_uniform
3.2.1.1 Solution solution
Python
from hydrogen import * from qmc_stats import * def MonteCarlo(a, nmax): energy = 0. normalization = 0. for istep in range(nmax): r = np.random.uniform(-5., 5., (3)) w = psi(a,r) w = w*w normalization += w energy += w * e_loc(a,r) return energy/normalization a = 0.9 nmax = 100000 X = [MonteCarlo(a,nmax) for i in range(30)] E, deltaE = ave_error(X) print(f"E = {E} +/- {deltaE}")
E = -0.4956255109300764 +/- 0.0007082875482711226
Fortran
When running Monte Carlo calculations, the number of steps is
usually very large. We expect nmax to be possibly larger than 2
billion, so we use 8-byte integers (integer*8) to represent it, as
well as the index of the current step.
subroutine uniform_montecarlo(a,nmax,energy) implicit none double precision, intent(in) :: a integer*8 , intent(in) :: nmax double precision, intent(out) :: energy integer*8 :: istep double precision :: norm, r(3), w double precision, external :: e_loc, psi energy = 0.d0 norm = 0.d0 do istep = 1,nmax call random_number(r) r(:) = -5.d0 + 10.d0*r(:) w = psi(a,r) w = w*w norm = norm + w energy = energy + w * e_loc(a,r) end do energy = energy / norm end subroutine uniform_montecarlo program qmc implicit none double precision, parameter :: a = 0.9 integer*8 , parameter :: nmax = 100000 integer , parameter :: nruns = 30 integer :: irun double precision :: X(nruns) double precision :: ave, err do irun=1,nruns call uniform_montecarlo(a,nmax,X(irun)) enddo call ave_error(X,nruns,ave,err) print *, 'E = ', ave, '+/-', err end program qmc
E = -0.49588321986667677 +/- 7.1758863546737969E-004
3.3 Metropolis sampling with \(\Psi^2\)
We will now use the square of the wave function to sample random points distributed with the probability density \[ P(\mathbf{r}) = \left[\Psi(\mathbf{r})\right]^2 \]
The expression of the average energy is now simplified as the average of the local energies, since the weights are taken care of by the sampling :
\[ E \approx \frac{1}{M}\sum_{i=1}^M E_L(\mathbf{r}_i) \]
To sample a chosen probability density, an efficient method is the Metropolis-Hastings sampling algorithm. Starting from a random initial position \(\mathbf{r}_0\), we will realize a random walk as follows:
\[ \mathbf{r}_{n+1} = \mathbf{r}_{n} + \tau \mathbf{u} \]
where \(\tau\) is a fixed constant (the so-called time-step), and \(\mathbf{u}\) is a uniform random number in a 3-dimensional box \((-1,-1,-1) \le \mathbf{u} \le (1,1,1)\). We will then add the accept/reject step that guarantees that the distribution of the \(\mathbf{r}_n\) is \(\Psi^2\):
- Compute \(\Psi\) at a new position \(\mathbf{r'} = \mathbf{r}_n + \tau \mathbf{u}\)
- Compute the ratio \(R = \frac{\left[\Psi(\mathbf{r'})\right]^2}{\left[\Psi(\mathbf{r}_{n})\right]^2}\)
- Draw a uniform random number \(v \in [0,1]\)
- if \(v \le R\), accept the move : set \(\mathbf{r}_{n+1} = \mathbf{r'}\)
- else, reject the move : set \(\mathbf{r}_{n+1} = \mathbf{r}_n\)
- evaluate the local energy at \(\mathbf{r}_{n+1}\)
A common error is to remove the rejected samples from the calculation of the average. Don't do it!
All samples should be kept, from both accepted and rejected moves.
If the time step is infinitely small, the ratio will be very close to one and all the steps will be accepted. But the trajectory will be infinitely too short to have statistical significance.
On the other hand, as the time step increases, the number of accepted steps will decrease because the ratios might become small. If the number of accepted steps is close to zero, then the space is not well sampled either.
The time step should be adjusted so that it is as large as possible, keeping the number of accepted steps not too small. To achieve that, we define the acceptance rate as the number of accepted steps over the total number of steps. Adjusting the time step such that the acceptance rate is close to 0.5 is a good compromise.
3.3.1 Exercise
Modify the program of the previous section to compute the energy, sampled with \(\Psi^2\).
Compute also the acceptance rate, so that you can adapt the time step in order to have an acceptance rate close to 0.5 .
Can you observe a reduction in the statistical error?
Python
from hydrogen import * from qmc_stats import * def MonteCarlo(a,nmax,tau): # TODO return energy/nmax, N_accep/nmax # Run simulation a = 0.9 nmax = 100000 tau = 1.3 X0 = [ MonteCarlo(a,nmax,tau) for i in range(30)] # Energy X = [ x for (x, _) in X0 ] E, deltaE = ave_error(X) print(f"E = {E} +/- {deltaE}") # Acceptance rate X = [ x for (_, x) in X0 ] A, deltaA = ave_error(X) print(f"A = {A} +/- {deltaA}")
Fortran
subroutine metropolis_montecarlo(a,nmax,tau,energy,accep) implicit none double precision, intent(in) :: a integer*8 , intent(in) :: nmax double precision, intent(in) :: tau double precision, intent(out) :: energy double precision, intent(out) :: accep integer*8 :: istep double precision :: r_old(3), r_new(3), psi_old, psi_new double precision :: v, ratio integer*8 :: n_accep double precision, external :: e_loc, psi, gaussian ! TODO end subroutine metropolis_montecarlo program qmc implicit none double precision, parameter :: a = 0.9d0 double precision, parameter :: tau = 1.3d0 integer*8 , parameter :: nmax = 100000 integer , parameter :: nruns = 30 integer :: irun double precision :: X(nruns), Y(nruns) double precision :: ave, err do irun=1,nruns call metropolis_montecarlo(a,nmax,tau,X(irun),Y(irun)) enddo call ave_error(X,nruns,ave,err) print *, 'E = ', ave, '+/-', err call ave_error(Y,nruns,ave,err) print *, 'A = ', ave, '+/-', err end program qmc
gfortran hydrogen.f90 qmc_stats.f90 qmc_metropolis.f90 -o qmc_metropolis ./qmc_metropolis
3.3.1.1 Solution solution
Python
from hydrogen import * from qmc_stats import * def MonteCarlo(a,nmax,tau): energy = 0. N_accep = 0 r_old = np.random.uniform(-tau, tau, (3)) psi_old = psi(a,r_old) for istep in range(nmax): r_new = r_old + np.random.uniform(-tau,tau,(3)) psi_new = psi(a,r_new) ratio = (psi_new / psi_old)**2 v = np.random.uniform() if v <= ratio: N_accep += 1 r_old = r_new psi_old = psi_new energy += e_loc(a,r_old) return energy/nmax, N_accep/nmax # Run simulation a = 0.9 nmax = 100000 tau = 1.3 X0 = [ MonteCarlo(a,nmax,tau) for i in range(30)] # Energy X = [ x for (x, _) in X0 ] E, deltaE = ave_error(X) print(f"E = {E} +/- {deltaE}") # Acceptance rate X = [ x for (_, x) in X0 ] A, deltaA = ave_error(X) print(f"A = {A} +/- {deltaA}")
E = -0.4950720838131573 +/- 0.00019089638602238043 A = 0.5172960000000001 +/- 0.0003443446549306529
Fortran
subroutine metropolis_montecarlo(a,nmax,tau,energy,accep) implicit none double precision, intent(in) :: a integer*8 , intent(in) :: nmax double precision, intent(in) :: tau double precision, intent(out) :: energy double precision, intent(out) :: accep integer*8 :: istep double precision :: r_old(3), r_new(3), psi_old, psi_new double precision :: v, ratio integer*8 :: n_accep double precision, external :: e_loc, psi, gaussian energy = 0.d0 n_accep = 0_8 call random_number(r_old) r_old(:) = tau * (2.d0*r_old(:) - 1.d0) psi_old = psi(a,r_old) do istep = 1,nmax call random_number(r_new) r_new(:) = r_old(:) + tau * (2.d0*r_new(:) - 1.d0) psi_new = psi(a,r_new) ratio = (psi_new / psi_old)**2 call random_number(v) if (v <= ratio) then r_old(:) = r_new(:) psi_old = psi_new n_accep = n_accep + 1_8 endif energy = energy + e_loc(a,r_old) end do energy = energy / dble(nmax) accep = dble(n_accep) / dble(nmax) end subroutine metropolis_montecarlo program qmc implicit none double precision, parameter :: a = 0.9d0 double precision, parameter :: tau = 1.3d0 integer*8 , parameter :: nmax = 100000 integer , parameter :: nruns = 30 integer :: irun double precision :: X(nruns), Y(nruns) double precision :: ave, err do irun=1,nruns call metropolis_montecarlo(a,nmax,tau,X(irun),Y(irun)) enddo call ave_error(X,nruns,ave,err) print *, 'E = ', ave, '+/-', err call ave_error(Y,nruns,ave,err) print *, 'A = ', ave, '+/-', err end program qmc
E = -0.49515370205041676 +/- 1.7660819245720729E-004 A = 0.51713866666666664 +/- 3.7072551835783688E-004
3.4 Gaussian random number generator
To obtain Gaussian-distributed random numbers, you can apply the Box Muller transform to uniform random numbers:
\begin{eqnarray*} z_1 &=& \sqrt{-2 \ln u_1} \cos(2 \pi u_2) \\ z_2 &=& \sqrt{-2 \ln u_1} \sin(2 \pi u_2) \end{eqnarray*}Below is a Fortran implementation returning a Gaussian-distributed n-dimensional vector \(\mathbf{z}\). This will be useful for the following sections.
Fortran
subroutine random_gauss(z,n) implicit none integer, intent(in) :: n double precision, intent(out) :: z(n) double precision :: u(n+1) double precision, parameter :: two_pi = 2.d0*dacos(-1.d0) integer :: i call random_number(u) if (iand(n,1) == 0) then ! n is even do i=1,n,2 z(i) = dsqrt(-2.d0*dlog(u(i))) z(i+1) = z(i) * dsin( two_pi*u(i+1) ) z(i) = z(i) * dcos( two_pi*u(i+1) ) end do else ! n is odd do i=1,n-1,2 z(i) = dsqrt(-2.d0*dlog(u(i))) z(i+1) = z(i) * dsin( two_pi*u(i+1) ) z(i) = z(i) * dcos( two_pi*u(i+1) ) end do z(n) = dsqrt(-2.d0*dlog(u(n))) z(n) = z(n) * dcos( two_pi*u(n+1) ) end if end subroutine random_gauss
In Python, you can use the random.normal function of Numpy.
3.5 Generalized Metropolis algorithm
One can use more efficient numerical schemes to move the electrons, but the Metropolis accepation step has to be adapted accordingly: the acceptance probability \(A\) is chosen so that it is consistent with the probability of leaving \(\mathbf{r}_n\) and the probability of entering \(\mathbf{r}_{n+1}\):
\[ A(\mathbf{r}_{n} \rightarrow \mathbf{r}_{n+1}) = \min \left( 1, \frac{T(\mathbf{r}_{n+1} \rightarrow \mathbf{r}_{n}) P(\mathbf{r}_{n+1})} {T(\mathbf{r}_{n} \rightarrow \mathbf{r}_{n+1}) P(\mathbf{r}_{n})} \right) \] where \(T(\mathbf{r}_n \rightarrow \mathbf{r}_{n+1})\) is the probability of transition from \(\mathbf{r}_n\) to \(\mathbf{r}_{n+1}\).
In the previous example, we were using uniform random numbers. Hence, the transition probability was
\[ T(\mathbf{r}_{n} \rightarrow \mathbf{r}_{n+1}) = \text{constant} \]
so the expression of \(A\) was simplified to the ratios of the squared wave functions.
Now, if instead of drawing uniform random numbers we choose to draw Gaussian random numbers with zero mean and variance \(\tau\), the transition probability becomes:
\[ T(\mathbf{r}_{n} \rightarrow \mathbf{r}_{n+1}) = \frac{1}{(2\pi\,\tau)^{3/2}} \exp \left[ - \frac{\left( \mathbf{r}_{n+1} - \mathbf{r}_{n} \right)^2}{2\tau} \right] \]
To sample even better the density, we can "push" the electrons into in the regions of high probability, and "pull" them away from the low-probability regions. This will mechanically increase the acceptance ratios and improve the sampling.
To do this, we can add the drift vector
\[ \frac{\nabla [ \Psi^2 ]}{\Psi^2} = 2 \frac{\nabla \Psi}{\Psi}. \]
The numerical scheme becomes a drifted diffusion:
\[ \mathbf{r}_{n+1} = \mathbf{r}_{n} + \tau \frac{\nabla \Psi(\mathbf{r})}{\Psi(\mathbf{r})} + \chi \]
where \(\chi\) is a Gaussian random variable with zero mean and variance \(\tau\). The transition probability becomes:
\[ T(\mathbf{r}_{n} \rightarrow \mathbf{r}_{n+1}) = \frac{1}{(2\pi\,\tau)^{3/2}} \exp \left[ - \frac{\left( \mathbf{r}_{n+1} - \mathbf{r}_{n} - \frac{\nabla \Psi(\mathbf{r}_n)}{\Psi(\mathbf{r}_n)} \right)^2}{2\,\tau} \right] \]
3.5.1 Exercise 1
Write a function to compute the drift vector \(\frac{\nabla \Psi(\mathbf{r})}{\Psi(\mathbf{r})}\).
Python
def drift(a,r): # TODO
Fortran
subroutine drift(a,r,b) implicit none double precision, intent(in) :: a, r(3) double precision, intent(out) :: b(3) ! TODO end subroutine drift
3.5.1.1 Solution solution
Python
def drift(a,r): ar_inv = -a/np.sqrt(np.dot(r,r)) return r * ar_inv
Fortran
subroutine drift(a,r,b) implicit none double precision, intent(in) :: a, r(3) double precision, intent(out) :: b(3) double precision :: ar_inv ar_inv = -a / dsqrt(r(1)*r(1) + r(2)*r(2) + r(3)*r(3)) b(:) = r(:) * ar_inv end subroutine drift
3.5.2 Exercise 2
Modify the previous program to introduce the drifted diffusion scheme. (This is a necessary step for the next section).
Python
from hydrogen import * from qmc_stats import * def MonteCarlo(a,nmax,tau): # TODO # Run simulation a = 0.9 nmax = 100000 tau = 1.3 X0 = [ MonteCarlo(a,nmax,tau) for i in range(30)] # Energy X = [ x for (x, _) in X0 ] E, deltaE = ave_error(X) print(f"E = {E} +/- {deltaE}") # Acceptance rate X = [ x for (_, x) in X0 ] A, deltaA = ave_error(X) print(f"A = {A} +/- {deltaA}")
Fortran
subroutine variational_montecarlo(a,tau,nmax,energy,accep_rate) implicit none double precision, intent(in) :: a, tau integer*8 , intent(in) :: nmax double precision, intent(out) :: energy, accep_rate integer*8 :: istep double precision :: sq_tau, chi(3) double precision :: psi_old, psi_new double precision :: r_old(3), r_new(3) double precision :: d_old(3), d_new(3) double precision, external :: e_loc, psi ! TODO end subroutine variational_montecarlo program qmc implicit none double precision, parameter :: a = 0.9 double precision, parameter :: tau = 1.0 integer*8 , parameter :: nmax = 100000 integer , parameter :: nruns = 30 integer :: irun double precision :: X(nruns), accep(nruns) double precision :: ave, err do irun=1,nruns call variational_montecarlo(a,tau,nmax,X(irun),accep(irun)) enddo call ave_error(X,nruns,ave,err) print *, 'E = ', ave, '+/-', err call ave_error(accep,nruns,ave,err) print *, 'A = ', ave, '+/-', err end program qmc
gfortran hydrogen.f90 qmc_stats.f90 vmc_metropolis.f90 -o vmc_metropolis ./vmc_metropolis
3.5.2.1 Solution solution
Python
from hydrogen import * from qmc_stats import * def MonteCarlo(a,nmax,tau): energy = 0. accep_rate = 0. sq_tau = np.sqrt(tau) r_old = np.random.normal(loc=0., scale=1.0, size=(3)) d_old = drift(a,r_old) d2_old = np.dot(d_old,d_old) psi_old = psi(a,r_old) for istep in range(nmax): chi = np.random.normal(loc=0., scale=1.0, size=(3)) r_new = r_old + tau * d_old + sq_tau * chi d_new = drift(a,r_new) d2_new = np.dot(d_new,d_new) psi_new = psi(a,r_new) # Metropolis prod = np.dot((d_new + d_old), (r_new - r_old)) argexpo = 0.5 * (d2_new - d2_old)*tau + prod q = psi_new / psi_old q = np.exp(-argexpo) * q*q if np.random.uniform() < q: accep_rate += 1. r_old = r_new d_old = d_new d2_old = d2_new psi_old = psi_new energy += e_loc(a,r_old) return energy/nmax, accep_rate/nmax # Run simulation a = 0.9 nmax = 100000 tau = 1.3 X0 = [ MonteCarlo(a,nmax,tau) for i in range(30)] # Energy X = [ x for (x, _) in X0 ] E, deltaE = ave_error(X) print(f"E = {E} +/- {deltaE}") # Acceptance rate X = [ x for (_, x) in X0 ] A, deltaA = ave_error(X) print(f"A = {A} +/- {deltaA}")
E = -0.4951317910667116 +/- 0.00014045774335059988 A = 0.7200673333333333 +/- 0.00045942791345632793
Fortran
subroutine variational_montecarlo(a,tau,nmax,energy,accep_rate) implicit none double precision, intent(in) :: a, tau integer*8 , intent(in) :: nmax double precision, intent(out) :: energy, accep_rate integer*8 :: istep double precision :: sq_tau, chi(3), d2_old, prod, u double precision :: psi_old, psi_new, d2_new, argexpo, q double precision :: r_old(3), r_new(3) double precision :: d_old(3), d_new(3) double precision, external :: e_loc, psi sq_tau = dsqrt(tau) ! Initialization energy = 0.d0 accep_rate = 0.d0 call random_gauss(r_old,3) call drift(a,r_old,d_old) d2_old = d_old(1)*d_old(1) + d_old(2)*d_old(2) + d_old(3)*d_old(3) psi_old = psi(a,r_old) do istep = 1,nmax call random_gauss(chi,3) r_new(:) = r_old(:) + tau * d_old(:) + chi(:)*sq_tau call drift(a,r_new,d_new) d2_new = d_new(1)*d_new(1) + d_new(2)*d_new(2) + d_new(3)*d_new(3) psi_new = psi(a,r_new) ! Metropolis prod = (d_new(1) + d_old(1))*(r_new(1) - r_old(1)) + & (d_new(2) + d_old(2))*(r_new(2) - r_old(2)) + & (d_new(3) + d_old(3))*(r_new(3) - r_old(3)) argexpo = 0.5d0 * (d2_new - d2_old)*tau + prod q = psi_new / psi_old q = dexp(-argexpo) * q*q call random_number(u) if (u<q) then accep_rate = accep_rate + 1.d0 r_old(:) = r_new(:) d_old(:) = d_new(:) d2_old = d2_new psi_old = psi_new end if energy = energy + e_loc(a,r_old) end do energy = energy / dble(nmax) accep_rate = dble(accep_rate) / dble(nmax) end subroutine variational_montecarlo program qmc implicit none double precision, parameter :: a = 0.9 double precision, parameter :: tau = 1.0 integer*8 , parameter :: nmax = 100000 integer , parameter :: nruns = 30 integer :: irun double precision :: X(nruns), accep(nruns) double precision :: ave, err do irun=1,nruns call variational_montecarlo(a,tau,nmax,X(irun),accep(irun)) enddo call ave_error(X,nruns,ave,err) print *, 'E = ', ave, '+/-', err call ave_error(accep,nruns,ave,err) print *, 'A = ', ave, '+/-', err end program qmc
E = -0.49495906384751226 +/- 1.5257646086088266E-004 A = 0.78861366666666666 +/- 3.7855335138754813E-004
4 Diffusion Monte Carlo
4.1 Schrödinger equation in imaginary time
Consider the time-dependent Schrödinger equation:
\[ i\frac{\partial \Psi(\mathbf{r},t)}{\partial t} = \hat{H} \Psi(\mathbf{r},t) \]
We can expand \(\Psi(\mathbf{r},0)\), in the basis of the eigenstates of the time-independent Hamiltonian:
\[ \Psi(\mathbf{r},0) = \sum_k a_k\, \Phi_k(\mathbf{r}). \]
The solution of the Schrödinger equation at time \(t\) is
\[ \Psi(\mathbf{r},t) = \sum_k a_k \exp \left( -i\, E_k\, t \right) \Phi_k(\mathbf{r}). \]
Now, let's replace the time variable \(t\) by an imaginary time variable \(\tau=i\,t\), we obtain
\[ -\frac{\partial \psi(\mathbf{r}, \tau)}{\partial \tau} = \hat{H} \psi(\mathbf{r}, \tau) \]
where \(\psi(\mathbf{r},\tau) = \Psi(\mathbf{r},-i\tau) = \Psi(\mathbf{r},t)\) and \[ \psi(\mathbf{r},\tau) = \sum_k a_k \exp( -E_k\, \tau) \phi_k(\mathbf{r}). \] For large positive values of \(\tau\), \(\psi\) is dominated by the \(k=0\) term, namely the lowest eigenstate. So we can expect that simulating the differetial equation in imaginary time will converge to the exact ground state of the system.
4.2 Diffusion and branching
The diffusion equation of particles is given by
\[ \frac{\partial \phi(\mathbf{r},t)}{\partial t} = D\, \Delta \phi(\mathbf{r},t). \]
The rate of reaction \(v\) is the speed at which a chemical reaction takes place. In a solution, the rate is given as a function of the concentration \([A]\) by
\[ v = \frac{d[A]}{dt}, \]
where the concentration \([A]\) is proportional to the number of particles.
These two equations allow us to interpret the Schrödinger equation in imaginary time as the combination of:
- a diffusion equation with a diffusion coefficient \(D=1/2\) for the kinetic energy, and
- a rate equation for the potential.
The diffusion equation can be simulated by a Brownian motion: \[ \mathbf{r}_{n+1} = \mathbf{r}_{n} + \sqrt{\tau}\, \chi \] where \(\chi\) is a Gaussian random variable, and the rate equation can be simulated by creating or destroying particles over time (a so-called branching process).
Diffusion Monte Carlo (DMC) consists in obtaining the ground state of a system by simulating the Schrödinger equation in imaginary time, by the combination of a diffusion process and a branching process.
4.3 Importance sampling
In a molecular system, the potential is far from being constant, and diverges at inter-particle coalescence points. Hence, when the rate equation is simulated, it results in very large fluctuations in the numbers of particles, making the calculations impossible in practice. Fortunately, if we multiply the Schrödinger equation by a chosen trial wave function \(\Psi_T(\mathbf{r})\) (Hartree-Fock, Kohn-Sham determinant, CI wave function, etc), one obtains
\[ -\frac{\partial \psi(\mathbf{r},\tau)}{\partial \tau} \Psi_T(\mathbf{r}) = \left[ -\frac{1}{2} \Delta \psi(\mathbf{r},\tau) + V(\mathbf{r}) \psi(\mathbf{r},\tau) \right] \Psi_T(\mathbf{r}) \]
Defining \(\Pi(\mathbf{r},t) = \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r})\),
\[ -\frac{\partial \Pi(\mathbf{r},\tau)}{\partial \tau} = -\frac{1}{2} \Delta \Pi(\mathbf{r},\tau) + \nabla \left[ \Pi(\mathbf{r},\tau) \frac{\nabla \Psi_T(\mathbf{r})}{\Psi_T(\mathbf{r})} \right] + E_L(\mathbf{r}) \Pi(\mathbf{r},\tau) \]
The new "potential" is the local energy, which has smaller fluctuations as \(\Psi_T\) tends to the exact wave function. The new "kinetic energy" can be simulated by the drifted diffusion scheme presented in the previous section (VMC).
4.3.1 Appendix : Details of the Derivation
\[ -\frac{\partial \psi(\mathbf{r},\tau)}{\partial \tau} \Psi_T(\mathbf{r}) = \left[ -\frac{1}{2} \Delta \psi(\mathbf{r},\tau) + V(\mathbf{r}) \psi(\mathbf{r},\tau) \right] \Psi_T(\mathbf{r}) \]
\[ -\frac{\partial \big[ \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big]}{\partial \tau} = -\frac{1}{2} \Big( \Delta \big[ \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big] - \psi(\mathbf{r},\tau) \Delta \Psi_T(\mathbf{r}) - 2 \nabla \psi(\mathbf{r},\tau) \nabla \Psi_T(\mathbf{r}) \Big) + V(\mathbf{r}) \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \]
\[ -\frac{\partial \big[ \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big]}{\partial \tau} = -\frac{1}{2} \Delta \big[\psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big] + \frac{1}{2} \psi(\mathbf{r},\tau) \Delta \Psi_T(\mathbf{r}) + \Psi_T(\mathbf{r})\nabla \psi(\mathbf{r},\tau) \frac{\nabla \Psi_T(\mathbf{r})}{\Psi_T(\mathbf{r})} + V(\mathbf{r}) \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \]
\[ -\frac{\partial \big[ \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big]}{\partial \tau} = -\frac{1}{2} \Delta \big[\psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big] + \psi(\mathbf{r},\tau) \Delta \Psi_T(\mathbf{r}) + \Psi_T(\mathbf{r})\nabla \psi(\mathbf{r},\tau) \frac{\nabla \Psi_T(\mathbf{r})}{\Psi_T(\mathbf{r})} + E_L(\mathbf{r}) \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \] \[ -\frac{\partial \big[ \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big]}{\partial \tau} = -\frac{1}{2} \Delta \big[\psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \big] + \nabla \left[ \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \frac{\nabla \Psi_T(\mathbf{r})}{\Psi_T(\mathbf{r})} \right] + E_L(\mathbf{r}) \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r}) \]
Defining \(\Pi(\mathbf{r},t) = \psi(\mathbf{r},\tau) \Psi_T(\mathbf{r})\),
\[ -\frac{\partial \Pi(\mathbf{r},\tau)}{\partial \tau} = -\frac{1}{2} \Delta \Pi(\mathbf{r},\tau) + \nabla \left[ \Pi(\mathbf{r},\tau) \frac{\nabla \Psi_T(\mathbf{r})}{\Psi_T(\mathbf{r})} \right] + E_L(\mathbf{r}) \Pi(\mathbf{r},\tau) \]
4.4 TODO Hydrogen atom
4.4.1 Exercise
Modify the Metropolis VMC program to introduce the PDMC weight. In the limit \(\tau \rightarrow 0\), you should recover the exact energy of H for any value of \(a\).
4.4.1.1 Python
from hydrogen import * from qmc_stats import * def MonteCarlo(a,nmax,tau,Eref): energy = 0. normalization = 0. accep_rate = 0 sq_tau = np.sqrt(tau) r_old = np.random.normal(loc=0., scale=1.0, size=(3)) d_old = drift(a,r_old) d2_old = np.dot(d_old,d_old) psi_old = psi(a,r_old) w = 1.0 for istep in range(nmax): chi = np.random.normal(loc=0., scale=1.0, size=(3)) el = e_loc(a,r_old) w *= np.exp(-tau*(el - Eref)) normalization += w energy += w * el r_new = r_old + tau * d_old + sq_tau * chi d_new = drift(a,r_new) d2_new = np.dot(d_new,d_new) psi_new = psi(a,r_new) # Metropolis prod = np.dot((d_new + d_old), (r_new - r_old)) argexpo = 0.5 * (d2_new - d2_old)*tau + prod q = psi_new / psi_old q = np.exp(-argexpo) * q*q # PDMC weight if np.random.uniform() < q: accep_rate += 1 r_old = r_new d_old = d_new d2_old = d2_new psi_old = psi_new return energy/normalization, accep_rate/nmax a = 0.9 nmax = 10000 tau = .1 E_ref = -0.5 X = [MonteCarlo(a,nmax,tau,E_ref) for i in range(30)] E, deltaE = ave_error([x[0] for x in X]) A, deltaA = ave_error([x[1] for x in X]) print(f"E = {E} +/- {deltaE}\nA = {A} +/- {deltaA}")
4.4.1.2 Fortran
subroutine variational_montecarlo(a,tau,nmax,energy,accep_rate) implicit none double precision, intent(in) :: a, tau integer*8 , intent(in) :: nmax double precision, intent(out) :: energy, accep_rate integer*8 :: istep double precision :: norm, sq_tau, chi(3), d2_old, prod, u double precision :: psi_old, psi_new, d2_new, argexpo, q double precision :: r_old(3), r_new(3) double precision :: d_old(3), d_new(3) double precision, external :: e_loc, psi sq_tau = dsqrt(tau) ! Initialization energy = 0.d0 norm = 0.d0 accep_rate = 0.d0 call random_gauss(r_old,3) call drift(a,r_old,d_old) d2_old = d_old(1)*d_old(1) + d_old(2)*d_old(2) + d_old(3)*d_old(3) psi_old = psi(a,r_old) do istep = 1,nmax call random_gauss(chi,3) r_new(:) = r_old(:) + tau * d_old(:) + chi(:)*sq_tau call drift(a,r_new,d_new) d2_new = d_new(1)*d_new(1) + d_new(2)*d_new(2) + d_new(3)*d_new(3) psi_new = psi(a,r_new) ! Metropolis prod = (d_new(1) + d_old(1))*(r_new(1) - r_old(1)) + & (d_new(2) + d_old(2))*(r_new(2) - r_old(2)) + & (d_new(3) + d_old(3))*(r_new(3) - r_old(3)) argexpo = 0.5d0 * (d2_new - d2_old)*tau + prod q = psi_new / psi_old q = dexp(-argexpo) * q*q call random_number(u) if (u<q) then accep_rate = accep_rate + 1.d0 r_old(:) = r_new(:) d_old(:) = d_new(:) d2_old = d2_new psi_old = psi_new end if norm = norm + 1.d0 energy = energy + e_loc(a,r_old) end do energy = energy / norm accep_rate = accep_rate / norm end subroutine variational_montecarlo program qmc implicit none double precision, parameter :: a = 0.9 double precision, parameter :: tau = 1.0 integer*8 , parameter :: nmax = 100000 integer , parameter :: nruns = 30 integer :: irun double precision :: X(nruns), accep(nruns) double precision :: ave, err do irun=1,nruns call variational_montecarlo(a,tau,nmax,X(irun),accep(irun)) enddo call ave_error(X,nruns,ave,err) print *, 'E = ', ave, '+/-', err call ave_error(accep,nruns,ave,err) print *, 'A = ', ave, '+/-', err end program qmc
gfortran hydrogen.f90 qmc_stats.f90 vmc_metropolis.f90 -o vmc_metropolis ./vmc_metropolis
E = -0.49499990423528023 +/- 1.5958250761863871E-004 A = 0.78861366666666655 +/- 3.5096729498002445E-004
4.5 TODO Dihydrogen
We will now consider the H2 molecule in a minimal basis composed of the \(1s\) orbitals of the hydrogen atoms:
\[ \Psi(\mathbf{r}_1, \mathbf{r}_2) = \exp(-(\mathbf{r}_1 - \mathbf{R}_A)) + \] where \(\mathbf{r}_1\) and \(\mathbf{r}_2\) denote the electron coordinates and \(\mathbf{R}_A\) and \(\mathbf{R}_B\) the coordinates of the nuclei.
5 TODO [0/1] Last things to do
[ ]Prepare 4 questions for the exam: multiple-choice questions with 4 possible answers. Questions should be independent because they will be asked in a random order.[ ]Propose a project for the students to continue the programs. Idea: Modify the program to compute the exact energy of the H\(_2\) molecule at $R$=1.4010 bohr. Answer: 0.17406 a.u.